Geometria Espacial
1. (UFPE) Determinar o número de arestas e de vértices de um poliedro convexo com seis faces quadrangulares e quatro faces triangulares.
Como cada aresta foi contada duas vezes, temos:
2A = 36 -> A = 18
Aplicando a relação de Euler, temos:
A + 2 = V + F -> 18 + 2 = V + 10 -> V = 10
Resposta: O poliedro tem 10 faces, 18 arestas e 10 vértices.
2. (UFMG) Achar a área total da superfície de um cilindro reto, sabendo que o raio da base é de 10cm e a altura é de 20cm.
A área de cada base é dada por Ab = PI x r2 = 3,14 x 100 = 314cm2. Quando planificamos a superfície lateral de um cilindro, obtemos um retângulo no qual os lados têm a mesma altura h do cilindro e o comprimento 2PIr da circunferência de uma das bases. Assim, C = 2 x 3,14 x 10 = 62,8cm. Desse modo, a área da superfície lateral é Al = 62,8 x 20 = 1.256cm2. Assim, a área total da superfície desse cilindro é At = 314 + 314 + 1.256, o que resulta em At = 1.884cm2
3. A pirâmide de Quéops, conhecida como a Grande Pirâmide, tem cerca de 230m de aresta na base e altura aproximada de 147m. Qual é o seu volume?
Solução:
4. A casquinha de um sorvete tem a forma de um cone reto. Sabendo que o raio da base mede 3cm e a altura é de 12cm. Qual é o volume da casquinha? r = 3cm
Solução:
A base do cone é um círculo de área: Ab = PI x r2 = 3,14 x 9 = 28,26cm2. Como o volume da casquinha é dado por V = 1/3 x Ab x h = 1/3 x 28,26 x 12, temos: V = 113,04cm3 5. Achar o volume de um prisma regular hexagonal, sabendo que as arestas da base medem 2m e sua altura é de 10m.
Solução:
Um hexágono regular pode ser decomposto em seis triângulos congruentes e eqüiláteros. Os lados dos triângulos medem 2m e sua altura mede sen 60º = h/2. Assim, V3/2 = h/2, o que dá h = V3m ou h = 1,7m. Então, a área de cada triângulo é dada por: At = (2 x 1,7)/2 = 1,7m2. Como são seis triângulos, temos: Ah = 6 x 1,7 = 10,2m2.
Assim, o volume do prisma é V = área da base x altura. Logo, V = 10,2 x 10 ou V = 102m3
Nota: V3 é a raíz quadrada de 3. / Os resultados são aproximados.
Matriz
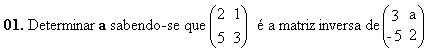
RESOLUÇÃO : a = -
2. Sejam as matrizes:
A= | 1 | 2 | 3 | B= | -2 | 0 | 1 | C= | -1 | D= | |||||||||
2 | -1 | 1 | 3 | 0 | 1 | 2 | 2 | -1 | |||||||||||
4 | |||||||||||||||||||
Basta adicionar elemento a elemento de A e B que ocupam a mesma posição na matriz. |
a)
A+B= | -1 | 2 | 4 |
5 | -1 | 2 |
3) Escreva na forma explícita as matrizes:
a) {aij} de ordem 3 x 5
4) Escreva explicitamente a matriz A=(a
ij) nos seguintes casos:
a) A é de ordem 3 x 2 com a
ij = i – j + 3
b) A é quadrada de ordem 3 com a
ij = 2i + j para i = j e
2i – j para i diferente de j
Sistema Linear
1 - Se o terno ordenado (2, 5, p) é solução da equação linear 6x - 7y + 2z = 5, qual o valor de p?
Solução: Teremos por simples substituição, observando que x = 2, y = 5 e z = p,
6.2 -7.5 + 2.p = 5. Logo, 12 - 35 + 2p = 5. Daí vem imediatamente que 2p = 28 e portanto, p = 14.
2 - Escreva a solução genérica para a equação linear 5x - 2y + z = 14, sabendo que o terno ordenado
(a , b , g ) é solução.
Solução: Podemos escrever: 5a - 2b + g = 14. Daí, tiramos: g = 14 - 5a + 2b . Portanto, a solução genérica será o terno ordenado (a , b , 14 - 5a + 2b ).
Observe que arbitrando-se os valores para a e b , a terceira variável ficará determinada em função desses valores. Por exemplo, fazendo-se a = 1, b = 3, teremos
g = 14 - 5a + 2b = 14 - 5.1 + 2.3 = 15, ou seja, o terno (1, 3, 15) é solução, e assim, sucessivamente. Verificamos pois que existem infinitas soluções para a equação linear dada, sendo o terno ordenado
(a , b , 14 - 5a + 2b ) a solução genérica.
3 - Qual o conjunto solução da equação linear 0x + 0y + 0z = 1?
Resp : S = f
4 - Determine o valor de 6p, sabendo-se que a quadra ordenada (2, p, -3, p+3) é solução da equação
3x + 4y - 5z + 2t = 10.
Resp : -17
Determinantes
1 - (FGV-2005) As meninas 1 = Adriana; 2 = Bruna e 3 = Carla falam muito ao telefone entre si. A matriz M mostra cada elemento aij representando o número de telefonemas que “i” deu para “j” no mês de setembro: Quem mais telefonou e quem mais recebeu ligações?
M= | 0 13 10|
|18 0 6 |
|9 12 0 |
Solução. Observe que a diagonal nula informa que ninguém ligou para si mesmo e, obviamente, não recebeu ligação de si mesmo. Decodificando os valores das posições:
M= | 0 13 10|
|18 0 6 |
|9 12 0 |
Solução. Observe que a diagonal nula informa que ninguém ligou para si mesmo e, obviamente, não recebeu ligação de si mesmo. Decodificando os valores das posições:
a) Adriana fez 23 ligações: 13 para Bruna e 10 para Carla.
b) Bruna fez 24 ligações: 18 para Adriana e 6 para Carla.
c) Carla fez 21 ligações: 9 para Adriana e 12 para Bruna.
d) Bruna foi quem mais telefonou. E recebeu 13 + 12 = 25 ligações.
e) Adriana foi a 2ª menina que mais ligou. E recebeu 18 + 9 = 27 ligações.
f) Carla foi quem menos ligou. E recebeu 10 + 6 = 16 ligações.
A resposta pedida é: Mais telefonou foi Bruna e recebeu mais ligações foi Adriana.
Números complexos
2 - Sendo z = 5i + 3i2 - 2i3 + 4i27 e w = 2i12 - 3i15 ,
calcule Im(z).w + Im(w).z .
3 - UCMG - O número complexo 2z, tal que 5z +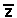
= 12 + 6i é:
4 - UCSal - Para que o produto (a+i). (3-2i) seja real, a deve ser:
5 - UFBA - Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de ac+b é:
6 - Mackenzie-SP - O valor da expressão y = i + i2 + i3 + ... + i1001 é:
Exercícios Resolvidos:
1) Sendo z = (m2 - 5m + 6) + (m2 - 1) i , determine m de modo que z seja um imaginário puro.
Solução: Para que o complexo z seja um imaginário puro, sua parte real deve ser nula ou seja, devemos ter
m2 - 5m + 6 = 0, que resolvida encontramos m=2 ou m=3.
m2 - 5m + 6 = 0, que resolvida encontramos m=2 ou m=3.
2) Determine a parte real do número complexo z = (1 + i)12 .
Solução: Observe que (1 + i)12 = [(1 + i)2]6 . Nestas condições, vamos desenvolver o produto notável
(1 + i)2 = 12 + 2.i + i2 = 1 + 2i -1 = 2i \ (1 + i)2 = 2i (isto é uma propriedade importante, que vale a pena ser memorizada).
Substituindo na expressão dada, vem:
(1 + i)12 = [(1 + i)2]6 = (2i)6 = 26.i6 = 64.(i2)3 = 64.(-1)3 = - 64.
Portanto, o número complexo dado fica z = - 64 = - 64 + 0i e portanto sua parte real é igual a-64.
(1 + i)2 = 12 + 2.i + i2 = 1 + 2i -1 = 2i \ (1 + i)2 = 2i (isto é uma propriedade importante, que vale a pena ser memorizada).
Substituindo na expressão dada, vem:
(1 + i)12 = [(1 + i)2]6 = (2i)6 = 26.i6 = 64.(i2)3 = 64.(-1)3 = - 64.
Portanto, o número complexo dado fica z = - 64 = - 64 + 0i e portanto sua parte real é igual a-64.
3) Determine a parte imaginária do número complexo z = (1 - i)200 .
Solução: Podemos escrever o complexo z como: z = [(1 - i)2]100 . Desenvolvendo o produto notável
(1 - i)2 = 12 - 2.i + i2 = 1 - 2i -1 = - 2i \ (1 - i)2 = - 2i (isto é uma propriedade importante, que merece ser memorizada).
Substituindo na expressão dada, vem:
z = (- 2i)100 = (- 2)100. i100 = 2100 . i100 = 2100 . ( i2 )50 = 2100. (- 1)50 = 2100 . 1 = 2100.
Logo, o número complexo z é igual a 2100 e portanto um número real. Daí concluímos que a sua parte imaginária é zero.
(1 - i)2 = 12 - 2.i + i2 = 1 - 2i -1 = - 2i \ (1 - i)2 = - 2i (isto é uma propriedade importante, que merece ser memorizada).
Substituindo na expressão dada, vem:
z = (- 2i)100 = (- 2)100. i100 = 2100 . i100 = 2100 . ( i2 )50 = 2100. (- 1)50 = 2100 . 1 = 2100.
Logo, o número complexo z é igual a 2100 e portanto um número real. Daí concluímos que a sua parte imaginária é zero.
Agora que você estudou a teoria, tente resolver os seguintes exercícios:
1 - Calcule o número complexo i126 + i-126 + i31 - i1802 - Sendo z = 5i + 3i2 - 2i3 + 4i27 e w = 2i12 - 3i15 ,
calcule Im(z).w + Im(w).z .
3 - UCMG - O número complexo 2z, tal que 5z +
= 12 + 6i é:4 - UCSal - Para que o produto (a+i). (3-2i) seja real, a deve ser:
5 - UFBA - Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de ac+b é:
6 - Mackenzie-SP - O valor da expressão y = i + i2 + i3 + ... + i1001 é:
